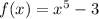Question

which function has an inverse function?/=means the _ of a fraction like 4_5F(X)= [x+3]/5F(X)=X^5-3F(X)=X^4/7 +27F(X)=1/x^2

Answer 1

Step 1. To find which function has an inverse function, we will use the horizontal line test.

Horizontal line test: If you draw a horizontal line and it touches the graph at two or more points, the function is not a one-to-one function, and therefore it does not have an inverse function.

For example:

Let's analyze the functions given in the options until we found the one that has an inverse function.

Step 2. The first function we have is:

`f(x)=(|x+3|)/(5)`

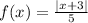
The graph of this function looks as follows:

We can draw a horizontal line and it will touch the graph at two points:

Therefore, the function is not a one-to-one function and it does not have an inverse function.

Step 3. The next function is:

`f(x)=x^5-3`

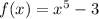
The graph looks as follows:

In this case, the horizontal lines will only touch the graph at one point:

Since it is a one-to-one function, it will have an inverse function.

Answer:

`f(x)=x^5-3`