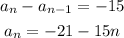Given: Given a sequence -36,-51,-66,-81....
Required: Recursive formula to represent the sequence.
Explanation:
For the given sequence,
Let us check the difference between consecutive terms.
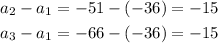
Thus, it is clearly an arithematic progression(A.P.) with first term a = -36 and common difference d = -15.
So let us find the nth term of the AP
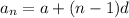
a = -36 and d = -15, so
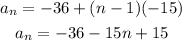
So
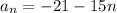
This is the formula for nth term.
Also,
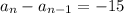
This is recursive formula.
Final Answer: