It is asked to determine the probability that a randomly selected club member prefers paperback books given that the club member reads about 1 hour per week. This can be mathematically represented as,
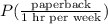
Apply Bayes' Theorem,

Thus, the required probability is 5/11.