Question

Consider F(x) = -2x^2 + 6. Which function describes the result of transforming through a reflection over the x-axis and a horizontal shift to the rightA.) G(x) = -2(x-1)^2 + 6B.) G(x) = 2(x-3)^2 + 6C.) H(x) = 2(x-5)^2 - 6D.) J(x) = -2(x+4)^2 + 6

Answer 1

To answer this question, we need to remember that:

1. If a function has been reflected in the x-axis, we have:

`-f(x)`

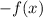
2. If a function has been translated by h units to the right, we have:

`f(x-h)`

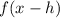
Therefore, if we have these two transformations on the function:

`f(x)=-2x^2+6`

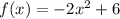
Then, if we apply the two transformations above, we have:

1. Reflection over the x-axis:

`F(x)=-2x^2+6\Rightarrow-F(x)=-(-2x^2+6)`

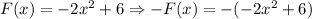
Therefore

`-F(x)=2x^2-6`

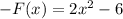
2. If we translate the function h units to the right, then we have:

`-F(x-h)=2(x-h)^2-6`

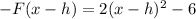
If we observe the options, we have that if we translate the function 5 units to the right, we have:

`-F(x-5)=2(x-5)^2-6`

In summary, therefore, we have that the function which describes the resulting transformation is:

`H(x)=2(x-5)^2-6`

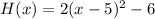
[Option C.]

We can see this in the following graph: the red parabola is the original function. The green parabola is the result of the transformation: