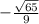Answer: sinθ =
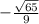
Explanation:
cosθ = 4/9
tan < 0
This means our reference angle is either in Quadrants II or IV, (where tangent is negative). Since cosine is positive, it must be Quadrant IV.
Therefore we know that sinθ will be negative.
we also know that
 , from the Pythagorean identities
, from the Pythagorean identities
.: 16/81 + sin^2(θ) = 1,
.: sinθ =
 =
=

But since this angle is in Quadrant IV, sinθ will be negative.
.: sinθ =