Question

Find the point of inflection of the graph of the function. (If an answer does not exist, enter DNE.)f(x) = x + 5 cos x, [0, 2]

Answer 1

`\begin{gathered} Inflection\:points: \\ ((\pi)/(2),(\pi)/(2)) \\ ((3\pi)/(2),(3\pi)/(2)) \\ Concave\:downward:\lbrack0,(\pi)/(2)\rbrack\cup((3\pi)/(2),2\pi\rbrack \\ Concave\:upward:((\pi)/(2),(3\pi)/(2)) \end{gathered}`

1) Since we need to find the inflection points, we need to take the second derivative of this function, and check whether f(x) is equal to zero or undefined.

`\begin{gathered} f`

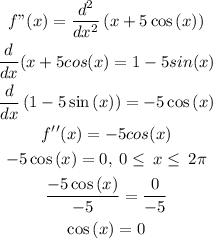
2) Now, we need to find the solutions for cos(x) within the given interval:

`\begin{gathered} cos(x)=0,0\leq x\leq2\pi \\ x=(\pi)/(2),\:x=(3\pi)/(2) \end{gathered}`

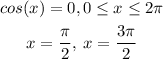
3) The next step is to find the y-coordinate, so let's plug each value of x we have just found into the original function:

`\begin{gathered} f(x)=x+5cos(x) \\ f((\pi)/(2))=((\pi)/(2))+5cos((\pi)/(2))\Rightarrow f(\pi/2)=(\pi)/(2) \\ \\ f((3\pi)/(2))=(3\pi)/(2)+5cos((3\pi)/(2))=(3\pi)/(2) \end{gathered}`

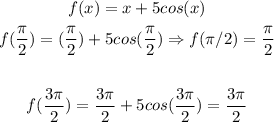
So the point of inflections are:

`\begin{gathered} \left((\pi)/(2),(\pi)/(2)\right) \\ \left((3\pi)/(2),(3\pi)/(2)\right) \end{gathered}`

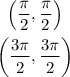
4) The Concavity can be found by combining the Domain with the inflection points, or we can also check them geometrically:

So, we can tell that:

`\begin{gathered} Concave\:downward:\lbrack0,(\pi)/(2)\rbrack\cup((3\pi)/(2),2\pi\rbrack \\ Concave\:upward:\:((\pi)/(2),(3\pi)/(2)) \end{gathered}`