Question

The distance between adjacent nodes in a standing wave pattern in a length of string is 25.0 cm:A. What is the wavelength of wave in the string?B. If the frequency of vibration is 200 Hz, calculate the velocity of the wave.

Answer 1

A) 50 cm

B) 10000 cm/s

Step-by-step explanation

Step 1

A)

If you know the distance between nodes and antinodes then use this equation:

`\begin{gathered} (\lambda)/(2)=D \\ \text{where}\lambda\text{ is the wavelength} \\ D\text{ is the distance betw}een\text{ nodes} \end{gathered}`

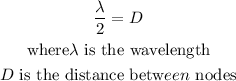
then, let

`D=\text{ 25 cm }`

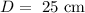
now, replace to find the wavelength

`\begin{gathered} (\lambda)/(2)=25 \\ \text{Multiply both sides by 2} \\ (\lambda)/(2)\cdot2=25\cdot2 \\ \lambda=50\text{ Cm} \end{gathered}`

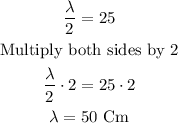
so, the wavelength is

A) 50 cm

Step 2

The speed of a wave can be found using the equation

`v=\lambda f`

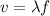
or velocity = wavelength x frequency,

then,let

`\begin{gathered} \lambda=50\text{ cm} \\ f=200\text{ Hz} \end{gathered}`

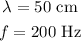
replace and evaluate

`\begin{gathered} v=\lambda f \\ v=50\text{ cm }\cdot200\text{ HZ} \\ v=10000\text{ }\frac{\text{cm}}{s} \end{gathered}`

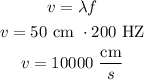
so

B) 10000 cm/s

I hope this helps you