Question

5#Suppose that scores on a particular test are normally distributed with a mean of 110 and a standard deviation of 15. What is the minimum score needed to be in the top 20% of the scores on the test? Carry your intermediate computations to at least four decimal places, and round your answer to one decimal place.

Answer 1

Let X be the random variable that describes the score of a randomly chosen student. We are told that X is distributed normally distributed with a mean of 110 and a standard deviation of 15. We want to be on the top 20% of the scores. So, we want to find the mininum x0 such that

`Pr(X\ge x_0)=0.2`

Let us calculate the following

`Z=\frac{X\text{ - 110}}{15}`

that is, we subtract the mean from X and divide it by the standard deviation. So we have that Z is normally distributed with mean 0 and standard deviation 1. So we have, in terms of Z that

`Pr(X\ge x_0)=Pr(Z\ge\frac{x_0\text{ -110}}{15})=0.2`

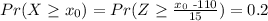
Let us call

`z_0=\frac{x_0\text{ -110}}{15}`

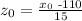
so now, we want to calculate z0. Using a table for the standard normal distribution we have that

`Pr(Z\ge z_0)=0.2`

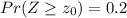
when z0 is approximately 0.84. So we have that

`z_0=0.84`

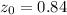
now, we replace that in our previous equation to get

`0.84=\frac{x_0\text{ -110}}{15}`

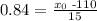
we multiply both sides by 15 to get

`x_0\text{ -110=0.84}\cdot15=12.6`

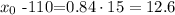
Finally, we add 110 on both sides so we get

`x_0=12.6+110=122.6`

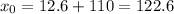
so the minimum score for being on the top 20% is 122.6