Question

A jumbo jet maintains a constant airspeed of 600 miles per hour (mi/hr) headed due north. The jet stream is 110 mi/hr in the northeasterly direction.(a) Express the velocity va of the jet relative to the air and the velocity vw of the jet stream in terms of i and j.(b) Find the velocity of the jet relative to the ground.(c) Find the actual speed and direction of the jet relative to the ground.

Answer 1

a)

If we consider i pointing to west-east direction and j pointing to south-north direction, since the airspeed is 600 miles per hour headed to north, the jet velocity relative to the air is given by:

`\vec{v_a}=600\hat{j}`

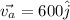
Since the jet stream is is 110 miles per hour in the northeasterly direction, we have:

`\begin{gathered} \vec{v_w}=110\cdot(\cos 45\degree\hat{i}+\sin 45\degree\hat{j}) \\ \vec{v_w}=55\sqrt[]{2}\hat{i}+55\sqrt[]{2}\hat{j} \end{gathered}`

b)

The velocity of the jet relative to the ground is given by:

`\begin{gathered} \vec{v_a}+\vec{v_w}=_{}55\sqrt[]{2}\hat{i}+(600+55\sqrt[]{2})\hat{j} \\ \vec{v_a}+\vec{v_w}=55\sqrt[]{2}\hat{i}+5(120+11\sqrt[]{2})\hat{j} \end{gathered}`

c)

Then, the actual speed of the jet relative to the ground is given by:

`\sqrt[]{\lbrack(55\sqrt[]{2})^2+(600+55\sqrt[]{2})^2}=\sqrt[]{372100+66000\sqrt[]{2}}=10\sqrt[]{3721+660\sqrt[]{2}}`

Finally, the direction of the jet relative to the ground is given by:

`\tan ^(-1)\frac{600+55\sqrt[]{2}}{55\sqrt[]{2}}=\tan ^(-1)((60)/(11)\sqrt[]{2}+1)`