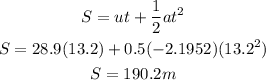Answer:
It takes the car 13.2 seconds to stop
The car travels 19.2 m while stopping
Step-by-step explanation:
The coefficient of kinetic friction, μ = 0.224
The initial velocity, u = 28.9 m/s
The final velocity, v = 0 m/s
The force acting in the x-direction is:
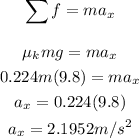
The time taken for the car to stop can be calculated using the formula:
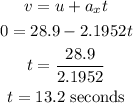
The distance travelled