Question

[Use g = 10 m/s2, use the values of sine, cosine, and tangent found on the AP Physics Table of Information.]On a long, level playfield, a player kicks a football with an initial speed of 20 m/s at an angle of 53° from the ground.(a) At what time does the ball reach its highest point?____ s(b) What is greatest height reached by the ball during projectile motion?____ m

Answer 1

(a) In order to determine the time at which the ball reaches its maximum height, use the following formula:

`v_y=v_(oy)-gt`

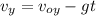
where,

vy: final speed at the maximum height = 0m/s

voy: vertical component of the initial velocity

g: gravitational acceleration constant = 9.8m/s^2

t: time

The vertical component of the initial velocity is:

`v_(oy)=v_o\sin (53)=((20m)/(s))(\sin (53))=(15.97m)/(s)`

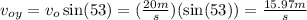
Solve the equation for t and replace the values of the rest of the parameters:

`t=(v_(oy)-v_y)/(g)=((15.97m)/(s)-(0m)/(s))/((9.8m)/(s^2))=1.63s`

Hence, after 1.63s the ball has reached its maximum height.

(ii) Use the following formula to determine the greatest height:

`y_(\max )=(v^2_(oy))/(2g)=(((15.97m)/(s))^2)/(2\cdot(9.8m)/(s^2))=13.01m`

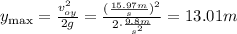
Hence, the maximum height is approximately 13.01m