ANSWER:
D) 134°
Explanation:
We have that the FEJ and GEI angles are equal, therefore:
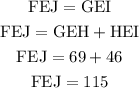
Now we have that the FEG and JEI angles are equal, we can calculate the value of these angles since we know that the sum of all the angles is equal to 360°, therefore:
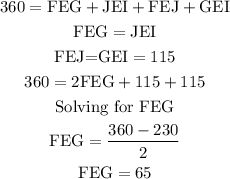
Now the value of FEH is equal to the sum of the FEG and GEH, we replace we have:
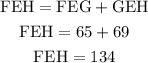
Which means that the angle FEH is 134°