Question

Car A travels 15 mph faster than Car B. In the same time that Car A travels 252 mi, Car B travels 216 mi. Find their speeds.The speed of Car Aisand the speed of Car B is

Answer 1

Speed is given by:

`V=\frac{change\text{ in position}}{change\text{ in time}}=(displacement)/(time)`

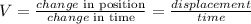
Let's call X the speed of car B in mph, then the speed of car A (let's call it Y) is given by x+15 mph.

The problem says car A travels 252 miles in the same time car B travels 216 miles. Then:

`\begin{gathered} X=\frac{216\text{ miles}}{t\text{ hours}}\text{ Eq.(1)} \\ Y=\frac{252\text{ miles}}{t\text{ hours}}\text{ Eq.(2)} \\ \text{Also we know that} \\ Y=X+15\text{ mph Eq.(3)} \\ As\text{ they travel the same time, let's solve for t in Eq(1) and Eq(2)} \\ t=(216)/(X) \\ t=(252)/(Y) \\ \text{Then if they travel the same time t=t, thus:} \\ (216)/(X)=(252)/(Y)\text{ Eq.(4)} \end{gathered}`

Now, replace Eq (3) into Eq(4) and solve for X:

`\begin{gathered} (216)/(X)=(252)/(X+15) \\ (216(X+15))/(X)=252 \\ (X+15)/(X)=(252)/(216) \\ \text{Applying the properties of fractions} \\ (X)/(X)+(15)/(X)=1.17 \\ 1+(15)/(X)=1.17 \\ (15)/(X)=1.17-1 \\ (15)/(X)=0.17 \\ 15=0.17X \\ X=(15)/(0.17) \\ X=90 \end{gathered}`

Then, car B travels at 90 mph, now replace this value into Eq (3) and solve for Y:

`\begin{gathered} Y=90+15 \\ Y=105 \end{gathered}`

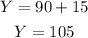
Thus, the speed of car A is 105 mph.

Answer: the speed of car A is 105 mph and the speed of car B is 90 moh.