Question

Y=4x^2-56x is the equation of a curve.

by completing the square, show that the co-ordinates of the turning point are (7,-196)

Answer 1

`y=4(x-7)^2-196`

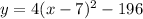
Explanation:

Given quadratic equation:

`y=4x^2-56x`

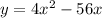
Completing the square

Factor out the coefficient of the term x²:

`y=4(x^2-14x)`

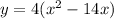
Add and subtract the square of half the coefficient of the term in x inside the brackets:

`y=4\left(x^2-14x+\left(-(14)/(2)\right)^2-\left(-(14)/(2)\right)^2\right)`

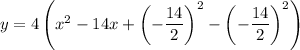
Simplify:

`y=4\left(x^2-14x+\left(-7\right)^2-\left(-7\right)^2\right)`

`y=4\left(x^2-14x+49-49\right)`

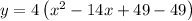
Factor the perfect square trinomial created by the first three terms inside the brackets:

`y=4\left((x-7)^2-49\right)`

Distribute:

`y=4(x-7)^2-196`

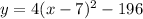
Turning point

The equation is now in vertex form y = a(x - h)² + k, where (h, k) is the vertex of the parabola (turning point).

Compare the equation with the vertex formula to identify the values of h and k:

• h = 7
• k = -196

Therefore, the coordinates of the turning point (vertex) are (7, -196).