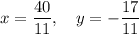Question

Solve each system by elimination -6x+4y=-28 and 6x+7y=11

Answer 1

`x=(40)/(11), \quad y=-(17)/(11)`

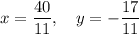
Explanation:

Given system of equations:

`\begin{cases}-6x+4y=-28\\6x+7y=11\end{cases}`

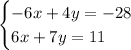
To solve by the method of elimination, add the equations together to eliminate the terms in x.

`\begin{array}{crcccl}&-6x & + & 4y & = & -28\\+&(6x & +&7y&=&\;\;\:11)\\\cline{2-6}\vphantom{\frac12}&&&11y&=&-17\\\cline{2-6}\end{array}`

Solve the equation for y:

`\implies y=-(17)/(11)`

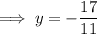
Substitute the found value of y into one of the equations and solve for x:

`\implies 6x+7\left(-(17)/(11)\right)=11`

`\implies 6x-(119)/(11)=11`

`\implies 6x=(240)/(11)`

`\implies x=(240)/(11\cdot 6)`

`\implies x=(40 \cdot \diagup\!\!\!\!\!6)/(11\cdot \diagup\!\!\!\!\!6)`

`\implies x=(40)/(11)`

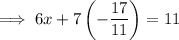
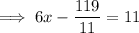
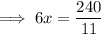
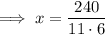
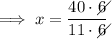
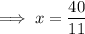
Therefore, the solution is:

`x=(40)/(11), \quad y=-(17)/(11)`