Answer:
18.7 units
Explanation:
In this right-angled triangle, you are provided with:
Two angles (i.e. 36° and 90°)
One side (i.e. Line AC, which is 11 units)
Line AB is known as the 'hypotenuse' of the right-angled triangle, which is what needs to be determined.
On the basis of 36° angle:
The side opposite (i.e. Line AC) is known as the 'opposite' or 'perpendicular side'
The side adjacent (i.e. Line BC) is known as the 'adjacent' or 'base'
Trigonometric function:
The trigonometric function, which connects an angle, it's opposite side and the hypotenuse is the 'sine function':
sinФ =
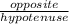
sin36° =

Cross-multiplication is applied:
x needs to be isolated and made the subject of the equation:
xsin36° = 11
≡ x =

∴ x = 18.7 units (Rounded off to 3 significant figures)