We have the differential equation,
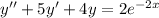 . The question asks to find the particular solution to the DE.
. The question asks to find the particular solution to the DE.
To find the particular solution look at the right-hand-side and make a “guess” of what the solution could be.
Since we have
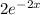 we can guess that the particular solution could be in the form
we can guess that the particular solution could be in the form
 , where
, where
 is some unknown constant.
is some unknown constant.
Now finding the value of the unknown constant,
 . Lets say
. Lets say
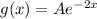 , find
, find
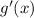 and
and
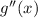 .
.
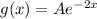
=>
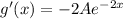
=>
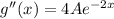
Now plug
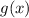 ,
,
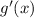 , and
, and
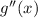 into the given differential equation.
into the given differential equation.
=>
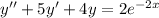
=>

=>
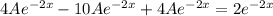
=>
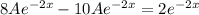
=>
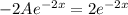
Compare the coefficients,
=>
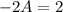
=>
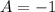
So we can say our "guess" to the particular solution of the given differential equation is,
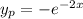 .
.