Question

Here 3 questions pls answer fast

Answer 1

Answers:

Question 3:
`((4)/(5)in.)/((2)/(3)hr.)`

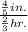
Question 4:
`(1)/(4)` ÷
`(2)/(5)`

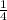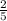
Question 5:
`(7)/(10)`

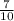
Explanations:

Question 3: We're told that rain is falling at a rate of
`(4)/(5) in.` every
`(2)/(3) hr.`, and the unit rate we're looking for is inches per hour (or more precisely, inches per 1 hour). Based on these parameters, we know that you have to divide the unit inches by the unit hours. So using the numbers above, the correct complex fraction to represent this situation would be
`((4)/(5) in.)/((2)/(3) hr.)` .

Question 4: In this question, we are given a complex fraction and asked to rewrite it as a simple division problem. The complex fraction is
`((1)/(4) km.)/((2)/(5) min.)`, so in order to write this as a division expression, you simply take the numerator fraction and divide it by the denominator fraction, which will end up being
`(1)/(4)` ÷
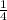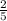`(2)/(5)`. Therefore, that will be your answer.

Question 5: Now, we have a division expression and are asked to use the Keep, Change, Flip method to solve the problem. First and foremost, the Keep, Change, Flip method is essentially telling you that when you are dividing by a fraction, you keep the dividend the same, you change the divisor - specifically switching the numerator with the denominator, which is creating the reciprocal of that fraction - and multiply by the reciprocal of the original divisor instead.

A good example of the Keep, Change, Flip method from above would be
`(1)/(2)` ÷
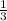`(1)/(3)`. You keep the dividend, change the divisor, specifically flip the function around to create its reciprocal, and instead multiply by the divisor's reciprocal. Following those steps,
`(1)/(2)` ÷
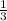`(1)/(3)` will become
`(1)/(2)` ×
`(3)/(1)` or
`(1)/(2)` ×
`3`.

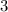Now that we understand how to use the Keep, Change, Flip method, we can use it to solve the expression
`(1)/(2)` ÷
`(5)/(7)`. We keep
`(1)/(2)` the same, flip
`(5)/(7)` to make its reciprocal, and multiply
`(1)/(2)` by that instead. So the final answer will be
`(1)/(2)` ÷
`(5)/(7)` =
`(1)/(2)` ×
`(7)/(5)` =
`(7)/(10)`.

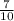Have a great day! Feel free to let me know if you have any more questions :)

Answer 2

Question 3

First option:

`\frac{\ensuremath{(4)/(5)\;in}}{(2)/(3)\;hr}`

Question 4
Third option:

`(1)/(4) / (2)/(5)`

Question 5

Second Option:

`(7)/(10)`

Explanation:

Question 3

If
`(4)/(5)` inches of rain falls every
`(2)/(3)` hours then the unit rate in inches per hour is inches
`/` hours

This would be:

`\frac{\ensuremath{(4)/(5)\;in}}{(2)/(3)\;hr}`

This is the first option in Question 3 answer choices

Question 4

`((1)/(4)\;km)/((2)/(5)\;min)`

is nothing but the numerator ÷ denominator which would be:

`(1)/(4) / (2)/(5)`

This is the third option in Question 4 answer choices

Question 5

`(1)/(2) / (5)/(7)\\`

Flip the divisor
`(5)/(7)`; it comes
`(7)/(5)`

Multiply:

`(1)/(2) * (7)/(5)`

The result is

`(7)/(10)`

This is the second option in Question 4 answer choices