Question

MODELING WITH MATHEMATICS Flying fish use their pectoral fins like airplane wings to glide through the air.a. Write an equation of the form y=a(x-h) = k with vertex (33,5) that models the flight path, assuming the fish leaves the water at . (0.0)b. What are the domain and range of the function? What do they represent in this situation? c. Does the value of a change when the flight path has vertex (30.4) ? Justify your answer.

Answer 1

a.
`y=-0.004591(x-33)^2+5`

b. domain: (0, 66) range (0, 5] and they represent how the vertical and horizontal distance will vary, so the domain (x-values) tells us the horizontal distance will vary from 0 to 66 during the flight path while the range (y-values) tell us the vertical distance or height will vary from 0 to 5 during the flight path.

c. the range will certainly change if the vertex is (30, 4) as the maximum is no longer 5, but rather 4, so the new range would be (0, 4]

Explanation:

So I'm assuming the form provided was meant to be written as:
`y=a(x-h)^2+k` also known as vertex form of a parabola. In this case the vertex is (33, 5) so we can plug these values into the equation:
`y=a(x-33)^2+5`

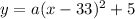
Now the only thing left to do is solve for the "a" value. We can just use a point on the graph except the vertex (since it makes the x-33 equal to zero making any value of "a" working) and we're given the point (0, 0) as a point so we can use that:

`0 = a(0-33)^2+5\\0 = 1,089a+5\\-5 = 1089a\\-0.004591 \approx a`

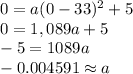
Now plug this value into the vertex form to get:

`y=-0.004591(x-33)^2+5`

Now using the quadratic formula:
`y=(-b\pm√(b^2-4ac))/(2a)` or a graphing calculator such as desmos, to determine the zeroes occur at x = 0 and 66. Since we want to only module their flight path the domain is restricted between these values, so the domain is: (0, 66) and the range is based on the y-values or in this case the height. The height will vary from zero to 5, or (0, 5]. They simply represent how the vertical and horizontal distance will vary, so the vertical distance will vary from 0 to 5 while the horizontal distance will vary from 0 to 66.

For part "c" I'm assuming it's asking if the domain/range change if the vertex is (30, 4) in which case the range will certainly change as the maximum is now 4 and not 5, so the new range would be (0, 4] where the vertical distance or height varies from 0 to 4