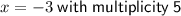Question

NO LINKS!!! (NOT MULTIPLE CHOICE)

1. Find the zeros of f(x), and state the multiplicity of each zero. (Order your answers from smallest to largest x.)

a. f(x) = 16x^5 + 56x^4 + 49x^3
x = ________ with multiplicity ________
x= ________ with multiplicity ________

b. f(x) = x(x + 3)^5 (3x - 7)^2
x = ___________ with multiplicity ___________
x = ___________ with multiplicity ___________
x= ___________ with multiplicity ___________

Answer 1

Part (a)

`x=0\; \sf with\;multiplicity\;1`

`x=-(7)/(4)\; \sf with\;multiplicity\;2`

Part (b)

`x=0\; \sf with\;multiplicity\;1`

`x=-3\; \sf with\;multiplicity\;5`

`x=(7)/(3)\; \sf with\;multiplicity\;2`

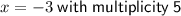
Explanation:

Part (a)

Given function:

`f(x) = 16x^5 + 56x^4 + 49x^3`

Factor out the common term x³:

`f(x) = x^3(16x^2 + 56x+ 49)`

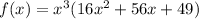
To factor the quadratic factor, rewrite in the form a² + 2ab + b²:

`\implies 16x^2+56x+49=(4x)^2+2 \cdot 4x \cdot 7+7^2`

Therefore:

• a = 4x
• b = 7

Apply the perfect square formula: a² + 2ab + b² = (a + b)²

`\implies 16x^2+56x+49=(4x+7)^2`

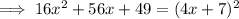
Therefore, the given function in fully factored form is:

`f(x)=x^3(4x+7)^2`

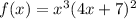
To find the zeros of the function, set the function to zero:

`x^3(4x+7)^2=0`

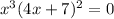
Apply the zero-product property:

`\implies x^3=0 \implies x=0`

`\implies (4x+7)^2=0 \implies x=-(7)/(4)`

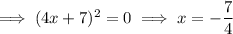
The multiplicity of a zero refers to the number of times the associated factor appears in the factored form of the equation of a polynomial.

As the factor (4x + 7) appears twice in the factored form of the polynomial, the associated zero has multiplicity 2.

Solution

`x=0\; \sf with\;multiplicity\;1`

`x=-(7)/(4)\; \sf with\;multiplicity\;2`

Part (b)

Given function:

`f(x) = x(x + 3)^5 (3x - 7)^2`

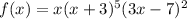
To find the zeros of the function, set the function to zero:

`x(x + 3)^5 (3x - 7)^2=0`

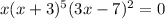
Apply the zero-product property:

`\implies x=0`

`\implies (x+3)^5=0 \implies x=-3`

`\implies (3x-7)^2=0 \implies x=(7)/(3)`

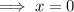
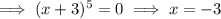
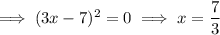
The multiplicity of a zero refers to the number of times the associated factor appears in the factored form of the equation of a polynomial.

As the factor (x + 3) appears five times in the factored form of the polynomial, the associated zero has multiplicity 5.

As the factor (3x - 7) appears twice in the factored form of the polynomial, the associated zero has multiplicity 2.

Solution

`x=0\; \sf with\;multiplicity\;1`

`x=-3\; \sf with\;multiplicity\;5`

`x=(7)/(3)\; \sf with\;multiplicity\;2`