Question

I need to find the variable that makes the equation true 5^6/5^m=5^9

Answer 1

Below

Explanation:

Re- arrange to

5^6 / 5^9 = 5 ^m

5^(6-9) = 5^m

5^-3 = 5^m show s m = -3

Answer 2

m = -3

Explanation:

The Quotient Rule of Exponents states that when dividing exponents with the same base, we should subtract the exponents.

`\boxed{(a^b)/(a^c)=a^(b-c)}`

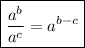
Given equation:

`(5^6)/(5^m)=5^9`

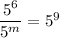
Apply the Quotient Rule to the given equation:

`\implies (5^6)/(5^m)=5^(6-m)`

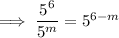
Therefore:

`\implies 5^(6-m)=5^9`

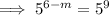
To find the value of m, equate the exponents and solve:

`\implies 6-m=9`

`\implies 6=9+m`

`\implies 6-9=m`

`\implies m=-3`

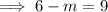
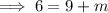
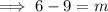
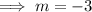
Therefore, the value of m that makes the equation true is m = -3.