Question

Find the volume V or radius r of the sphere. Round your answer to the nearest tenth, if necessary. Volume = 36 π m³​

Answer 1

The radius can be shown in 2 different forms

Fraction Form

`r=\sqrt[3]{(27)/(\pi)}`

Decimal Form

`r=2.05`

Explanation:

The formula for the volume of the sphere is

`V=(4)/(3)\pi r^3`

We are given the volume and we are asked to find the radius.

We can solve for
`r` in the equation for volume to evaluate the radius.

`(4)/(3)\pi r^3=V`

Move
`\pi` and
`r^3` into the numerator.

`(4\pi r^3)/(3)=V`

Divide both sides of the equation by 3.

`4\pi r^3=3V`

Divide both sides of the equation by
`4\pi`.

`r^3=(3V)/(4\pi )`

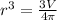
Take the cube root of both sides to eliminate the exponent.

`r=\sqrt[3]{(3V)/(4\pi )}`

Numerical Evaluation

Now we have an equation to evaluate
`r`.

Given
`V=36`

Insert 36 in for
`V`.

`r=\sqrt[3]{(3*36)/(4\pi )}`

Factor 4 out of
`3*36` and add parenthesis.

`r=\sqrt[3]{(4(3*9))/(4(\pi) )}`

Cancel the common factor of 4.

`r=\sqrt[3]{(3*9)/(\pi)}`

Multiply
`3*9`.

`r=\sqrt[3]{(27)/(\pi)}`

The answer can be shown in multiple forms.

Fraction Form

`r=\sqrt[3]{(27)/(\pi)}`

Decimal Form

`r=2.05`