Answer:
![5\cdot √(5)\cdot \sqrt[3]{x^4}\cdot y\cdot z^2](https://img.qammunity.org/2024/formulas/mathematics/high-school/zxt35sj7l6965jgf4esnp0nrt0nu9vcizg.png) =
=
![5\cdot √(5)\cdot x\sqrt[3]{x}\cdot y\cdot z^2](https://img.qammunity.org/2024/formulas/mathematics/high-school/zin4qirqqrvcpsj67z1ofklbmscvo3rqkw.png)
Explanation:
Let's take the individual terms and convert them to radical form
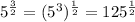
A term raised to the power 1/2 is nothing but the square root of that term
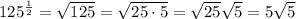
![x^{(4)/(3)} = (x^4)^{(1)/(3)} = \sqrt[3]{x^4}](https://img.qammunity.org/2024/formulas/mathematics/high-school/4u9szh98nr283onwy8u3n7iknvbjjw46h6.png) since any term raised to 1/3 is the cube root of that term
since any term raised to 1/3 is the cube root of that term
We can simplify this further by noting
 '
'
So
![\sqrt[3]{x^4} = \sqrt[3]{x^3} x = x\sqrt[3]{x}](https://img.qammunity.org/2024/formulas/mathematics/high-school/i3pyg8mvtqp2ft0um87uk5hu9ch7f2hzt3.png)
The other exponents are integers
Putting them all together we get
![5^{(3)/(2) }x^{(4)/(3)}yz^2 = 5\cdot √(5)\cdot x\sqrt[3]{x}\cdot y\cdot z^2](https://img.qammunity.org/2024/formulas/mathematics/high-school/sac1xl31hknpuyrwmp2vne205kd8gdlxyg.png)