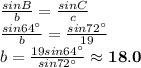Question

Consider a triangle ABC like the one below. Suppose that B=64°, C=72°, and c=19. (The figure is not drawn to scale.) Solve the triangle. Round your answers to the nearest tenth. I found angle A which is 44

Answer 1

`m\angle A = 44\textdegree, a = 13.9, b = 18.0`

Explanation:

Step 1: Solve for the Missing Angle

The measures of all of the interior angles of a triangle will always add up to
`180\textdegree`. Therefore,

`m\angle A = 180\textdegree - (m\angle B + m\angle C) = 180\textdegree - (64\textdegree + 72\textdegree) = 44\textdegree`

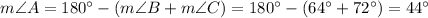
Step 2: Solve for the Missing Sides

When we are given the side lengths and angle measures of a triangle, we can use either the Law of Sines or the Law of Cosines to solve for the rest of the triangle.

The Law of Sines is as follows:
`(sinA)/(a) = (sinB)/(b) = (sinC)/(c)`

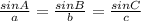
The Law of Cosines is as follows:
`c^(2) = a^(2) +b^(2) -2abcosC` (you can exchange c for a or b, respectively)

In this case, we are only given 1 side length and all 3 angle measures, so it would be more appropriate to use the Law of Sines as we need at least 2 side lengths to use the Law of Cosines.

Now that we know which formula to use, let's start by solving for
`a`, using the given values of
`c=19`,
`\angle A = 44\textdegree`, and
`\angle C = 72\textdegree`.

Substituting these values in, we get:

`(sinA)/(a) = (sinC)/(c) \\ (sin44\textdegree)/(a) = (sin72\textdegree)/(19)\\a=(19sin44\textdegree)/(sin72\textdegree) \approx \bf 13.9`

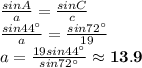
Repeating this process for
`b`, this time using
`\angle B = 64\textdegree`, we get:

`(sinB)/(b) = (sinC)/(c) \\ (sin64\textdegree)/(b) = (sin72\textdegree)/(19)\\b=(19sin64\textdegree)/(sin72\textdegree) \approx \bf 18.0`