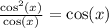Question

Simplify the following using trigonometric identities:
( 1 + sin (x) ) ( sec (x) - tan (x) )

Answer 1

`(1+\sin(x))(\sec(x)-\tan(x))=\cos(x)`

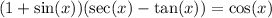
Explanation:

We are going to use the Pythagorean trigonometric identity:

`\sin^2(x)+\cos^2(x)=1`

and the following relationships between trigonometric functions:

`\sec(x)=(1)/(\cos(x))\\\tan(x)=(sin(x))/(cos(x))`

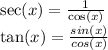
We can transform the expression as follows:

`(1+\sin(x))(\sec(x)-\tan(x))=(1+\sin(x))((1)/(\cos(x))-(\sin(x))/(\cos(x)))=(1+\sin(x))(1-\sin(x))/(\cos(x))=((1+\sin(x))(1-\sin(x)))/(\cos(x))`

Using the formula for the difference of two squares, we can write

`(1+\sin(x))(1-\sin(x))`

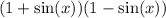
as

`1-\sin^2(x)`

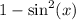
which, according to the Pythagorean trigonometric identity, is equal to

`\cos^2(x)`

Now we can simplify the original expression to

`(\cos^2(x))/(\cos(x))=\cos(x)`