Question

Determine the point P that

partitions the line segment AB
into the ratio 1:3 when A(2, 4)
and B(10, 8).

Answer 1

`\left((14)/(3)\;, \;(16)/(3)\right)`

Explanation:

We have two points A(2, 4) and B(10, 9)

P divides the segment AB, it is located 1/3 of the distance from A to B

Lets use the following notation

`\textsf {x_(AB)$= x-distance from A to B}`
This is the absolute difference between the x-coordinates of A and B

`\textsf {y_(AB)$= y-distance from A to B}`
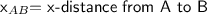
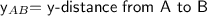
This is the absolute difference between the y-coordinates of A and B


`\textsf {x_(AP)$= x-distance from A to P}`
This is the absolute difference between the x-coordinates of A and P

`\textsf {y_(AP)$= y-distance from A to P}`
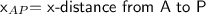
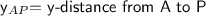
This is the absolute difference between the y-coordinates of A and P

To find the coordinates of P:

1. Find the x-distance between A and B:
   
   `\sf {x_(AB) } = 10 - 2\\\sf {x_(AB) } = 8\\\\`
   
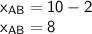
2. Find the y-distance between A and B:
   
   `\sf {y_(AB) } = 8 - 4\\\sf {y_(AB) } = 4\\\\`
   
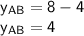
3. x-distance from A to P
   
   `\sf{x_(AP)=(1)/(3)x_(AB)}\\\\\sf{x_(AP)= (1)/(3) \cdot 8}\\\\\sf{x_(AP)= (8)/(3)`
   
   
4. y-distance from A to P is
   
   `\sf{y_(AP)=(1)/(3)y_(AB)}\\\\\sf{y_(AP)= (1)/(3) \cdot 4}\\\\\sf{y_(AP)= (4)/(3)`
   
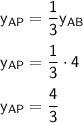
5. These values are relative to point A
   
6. Absolute x-value of P = x-value of A +
   `\sf{x_(AP)}`
   
   `= 2 + (8)/(3)\\\\= (14)/(3)\\`
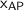
7. Absolute y-value of P = y-value of A +
   `\sf{y_(AP)}`
   
   `= 4 + (4)/(3)\\\\= (16)/(3)\\`

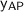
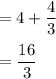
Answer: The coordinates of point P are:

`\left((14)/(3)\;, \;(16)/(3)\right)`

If you actually calculate the distances AB and AP using the distance formula:
`d = \sqrt {(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2}`

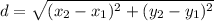
you will find
AB has length 8.944272 and AP has length 2.9829

2.9829/8.944272 ≅ 0.333 which is 1/3