Question

TRIGONOMETRY QUESTION-

alright my friend and i have been stuck on this FOREVER!
use properties of similar triangles to find the value of "x" and the length of the sides involving "x".
in this situation we are given two triangles, triangle ABC to triangle FEG (in that order, its weird, i know).
A = 5 F = 2x
B = x+4 E = 18
C = ? G = ?

I know usually you would set up the proportions, however when i do that i get 90=2x^2+8x, and i dont think i should be using the quadratic equation to find the side of a triangle. What is my best method of approach? if you leave the answer, please let me know how you did it!

Answer 1

You were on the right track, I totally understand why you'd get stuck where you are currently in the process. To start with, you technically found the wrong ratio between the two triangles. Your ratio is just 2x, while it should be 2x/5.

To start, let's find the ratio between triangle FEG and ABC by dividing angle F by and A:

`R=(2x)/(5)`

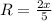
Now, multiply angle B by this ratio:

`(x+4)((2x)/(5) )=(2x^2)/(5)+(8x)/(5)=(2x^2+8x)/(5)`

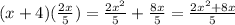
We can now set this expression equal to angle E, as we have multiplied by the common ratio:

`(2x^2+8x)/(5) =18`

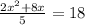
This looks rather daunting, but let's keep calm... you can do this!!

Start by subtracting 18 from both sides:

`(2x^2+8x)/(5)-18=0`

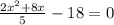
Now, let's get the whole expression under the denominator 5:

`(2x^2+8x-90)/(5)=0`

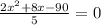
Notice that the denominator can now be removed:

`2x^2+8x-90=0`

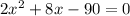
Now, factor the equation (you could also use the quadratic eq if you want)

`2(x-5)(x+9)=0`

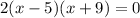
Notice that we have two potential values for x (5 and -9).

Think about this logically... If we use -9 and plug it in for x, we will end up with values of -5 degrees for an angle, which is impossible! Therefore 5 is the only valid answer!

I encourage you to also approach the problem from a different angle and use the common factor (5/2x) and multiply it by 18 :)