Answer:
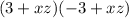

Explanation:
The Difference of Squares
Any difference of two squared monomial results in a factored form like shown below:
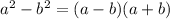
Similarly:

For a product of binomials to be a difference of squares, they must be in the described form.
------------------------
(x-y)(y-x) can be rewritten as:
-(x-y)(x-y)
Since both binomials are identicals, the product will not result in a difference of squares.
-----------------------
(6-y)(6-Y)
Since both binomials are identicals, the product will not result in a difference of squares.
-----------------------
(3+xz)(-3+xz) can be rewritten as:
(xz+3)(xz-3). This product is a sum multiplied by a difference of the very same terms, thus the result is a difference of squares:
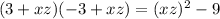
-----------------------
 . This product is a sum multiplied by a difference of the very same terms, thus the result is a difference of squares:
. This product is a sum multiplied by a difference of the very same terms, thus the result is a difference of squares:

-----------------------
Summarizing:
(3+xz)(-3+xz)
