Question

I have to get this done in one hour

Answer 1

23) m∠T = 20°

24) m∠ABC = 75°

Explanation:

Circle Theorem vocabulary

• Chord: a straight line joining two points on the circle.
• Inscribed angle: the angle formed when two chords meet at one point on a circle.
• Arc: the curve between two points on the circumference of a circle
• Intercepted arc: the arc that is between the endpoints of the chords that form the inscribed angle.

Question 23

Inscribed Angle Theorem

The measure of an inscribed angle is half the measure of the intercepted arc.

From inspection of the given circle, the inscribed angle is ∠T and the intercepted arc is RS. Therefore, applying the inscribed angle theorem:

`\implies m \angle T=(1)/(2)\overset{\frown}{RS}`

`\implies m \angle T=(1)/(2) \cdot 40^(\circ)`

`\implies m \angle T=20^(\circ)`

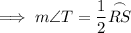
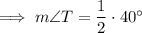
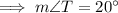
Therefore, the measure of ∠T is 20°.

Question 24

Quadrilateral ABCD is a cyclic quadrilateral since every vertex of the quadrilateral touches the circumference of the circle.

The opposite angles in a cyclic quadrilateral sum to 180°.

Therefore:

`\implies \angle A + \angle C = 180^(\circ)`

`\implies 10x^(\circ) + (4x+12)^(\circ) = 180^(\circ)`

`\implies 10x + 4x+12 = 180`

`\implies 14x+12 = 180`

`\implies 14x = 168`

`\implies x=12`

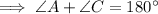
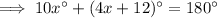
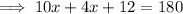
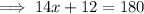
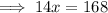
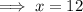
To calculate the measure of angle ABC, substitute the found value of x into the expression for ∠ABC:

`\implies \angle ABC=(6x+3)^(\circ)`

`\implies \angle ABC=(6(12)+3)^(\circ)`

`\implies \angle ABC=(72+3)^(\circ)`

`\implies \angle ABC=75^(\circ)`

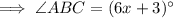
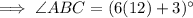
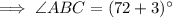
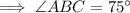
Therefore, the measure of ∠ABC is 75°.