Question

Question is attached. Show workings

Answer 1

C and A

Explanation:

We require to rationalise the denominators of the expressions by multiplying the numerator/ denominator by the conjugate of the denominator

given a + ib then conjugate is a - bi

note that i² = - 1

given

`(4+i)/(3-1)`

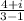
multiply numerator/denominator by 3 + i , the conjugate of 3 - i

=
`((4+i)(3+i))/((3-i)(3+i))` ← expand numerator/ denominator using FOIL

=
`(12+4i+3i+i^2)/(9+3i-3i-i^1)`

=
`(12+7i-1)/(9+1)`

=
`(11+7i)/(10)`

=
`(11)/(10)` +
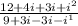
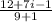
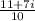
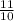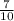`(7)/(10)` i ← in the form a + bi

with a =
`(11)/(10)`

----------------------------------------------------------------------------

`(1)/(1+i)`

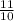
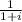
multiply numerator/denominator by 1 - i , the conjugate of 1 + 1

=
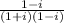`(1-i)/((1+i)(1-i))` ← expand denominator

=
`(1-i)/(1-i^2)`

=
`(1-i)/(1+1)`

=
`(1-i)/(2)`

=
`(1)/(2)` -
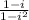
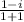
`(1)/(2)` i ← in the form a + bi ( b is the imaginary part )

with b = -
`(1)/(2)`