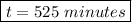Answer:
525 minutes
Explanation:
Let us find the temperature of each furnace after 't' minutes.
Furnace1:
Temperature in furnace1 is reducing at rate of 3.5°C per minute.
Rate of cooling after t minute = 3.5*t = 3.5t
We have to subtract 3.5t from 1200°C as it is cooling.
Temperature of furnace1 after 't' minutes = 1200 - 3.5t
Furance2:
Temperature in furnace2 is increasing at rate of 0.5°C per minute.
Rate of heating after t minute = 0.5*t = 0.5t
We have to add 3.5t from 900°C as it is getting heated.
Temperature of furnace1 after 't' minutes = 900 +0.5t
After some minutes, both furnace reach the same temperature.
900 + 0.5t = 1200 - 3.5t
900 + 0.5t + 3.5t = 1200
4t = 1200 + 900
4t = 2100
t = 2100 ÷ 4