The function in the given image that has a range limited to only negative numbers is
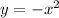 .
.
The range of a function is the set of all possible output values that the function can produce. For a function y = f(x), the range is defined as the set of all y-values such that there exists an x-value for which f(x) = y.
The function
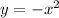 is a quadratic function, which means that its graph is a parabola. The parabola opens downwards, which means that all of its y-values are negative. Therefore, the range of the function is limited to only negative numbers.
is a quadratic function, which means that its graph is a parabola. The parabola opens downwards, which means that all of its y-values are negative. Therefore, the range of the function is limited to only negative numbers.
To see this mathematically, note that the equation
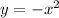 can be rewritten as
can be rewritten as
 . The square of any real number is always non-negative, so
. The square of any real number is always non-negative, so
 must always be negative. Therefore, the range of the function is limited to only negative numbers.
must always be negative. Therefore, the range of the function is limited to only negative numbers.
Here are some examples of input and output values for the function
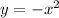
Input (x) Output (y)
-2 4
-1 1
0 0
1 -1
2 -4
As you can see, all of the output values are negative. Therefore, the range of the function is limited to only negative numbers.