Question

(2n²•n³•3n¹)²

(y•4y²)³


(4b³•b)²


(3s²•s³)²


(3r²•2r³)³


Simplify the exponents. Please show me how to do the step by step?? I'm not sure how to solve these when they have parentheses

Answer 1

(2n²•n³•3n¹)²

First, simplify inside the parentheses. We multiply the coefficients and exponents. The coefficients: 2×3=6. and the exponents: 2×3×1=6. All together that gives:
`(6n^6)^2`Then multiply the inside of the parentheses by itself since it's the exponent is 2. Therefore we end with
`36n^12`

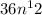
(y•4y²)³

Same approach. Multiply the inside which gives
`4y^3` Then calculate that to the power of 3.

`4y^3`×
`4y^3`×
`4y^3`=
`64y^9\\`

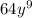
(4b³•b)²

`=(4b^4)^2\\=4b^4\cdot4b^4\\=16b^8`

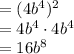
(3s²•s³)²

`=(3s^5)^2\\=3s^5\cdot3s^5\\=9s^(10)`

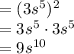
(3r²•2r³)³

`=(6r^5)^3\\=6r^5\cdot6r^5\cdot6r^5\\=216r^(15)`

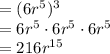
Hope that helped. Let me know if you have any further questions!