Question

Express (X+12)^2 standard form

Answer 1

`x^(2)+24x+144`

Explanation:

When multiplying two binomials, the FOIL (first, outer, inner, last) method is used for simplifying into standard form.

Our expression is
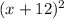`(x+12)^2`. This can be written as
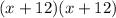`(x+12)(x+12)`, which now allows us to apply the FOIL method.

1. Multiply the first terms of both binomials together.

In
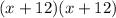`(x+12)(x+12)`, the first terms of both binomials are
`x`, which become
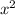`x^2` when multiplied together.

2. Multiply the outer terms of both binomials together and add it to what you have.

These are the terms on the left and right of the two binomials combined. The outer terms of
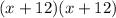`(x+12)(x+12)` are
`x` and
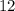`12`, which multiply to become
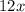`12x`. Now we add that to our result from the previous step, which gives us
`x^2 + 12x`.

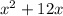3. Multiply the inner terms of both binomials together and add it to what you have.

These are the terms in the middle of the two binomials combined. The inner terms of
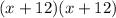`(x+12)(x+12)` are also
`x` and
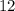`12`, which become
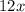`12x`. Adding it to our simplified expression so far, we get
`x^2 + 24x`.

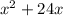4. Finally, multiply the last terms of both binomials together and add it to what you have.

In
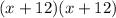`(x+12)(x+12)`, the last terms of both binomials are
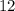`12`, which become
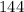`144` when multiplied together. Adding that to our simplified expression gives us
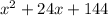`x^2 + 24x + 144`, our final answer in standard form.