Question

Please help me with this...​

Answer 1

`\boxed{x = 8 \;m}`

Explanation:

Nice drawing! :)

From the figure we see that the rectangle has a length of 30 m and a width of 20 m

The total area of the rectangle PQRS = 20 x 30 = 600 m²

The square footage of the planted area = area of figure MNSR = 388 m²

Therefore the rest of the area (the unshaded portion) is:
600 - 388 = 212 m²

This is the combined area of the two triangles ΔPNM and ΔMRG

Let's find the area of each of these triangles. Each of them is a right triangle which makes calculations easier

Area of a right triangle = (1/2) x base x height

ΔPNM has base = 30 - x and height = 20 -x

Area of ΔPNM

= (1/2) (30-x)(2-x)

We can use the FOIL method to evaluate (30-x)(2-x)

(30-x)(20-x)

= 30·20 + (30)(-x) + x(20) + (-x)(-x)

= 600 - 30x + 20x + x²

= 600 -50x + x³

We usually rewrite with coefficients in decreasing magnitude of x degree

Area of ΔPNM

`=(x^2 - 50x + 600)/(2)`

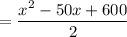
Let's now find the area of ΔMRQ with a base of x and a height of 20

Area of ΔMRQ

`=(1)/(2)\cdot 20 = (20x)/(2)`

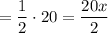
Adding both terms together we get

`(x^2 - 50x + 600)/(2) + (20x)/(2) \\`

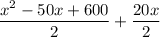
We have computed the area of the unshaded region as 212

So the above sum must be equal to 212

`(x^2 - 50x + 600)/(2) + (20x)/(2) = 212`

Multiply throughout by 2 to get rid of the denominator:

`\rightarrow \;\;x^2 - 50x + 600 + 20x = 212* 2 = 424\\\\\rightarrow \;\;x^2 -30x + 600 =424\\`

Move 424 to the left:

`x^2-30x+600-424=424-424\\\\x^2-30x+176=0`
`\textrm{Factoring } x^2-30x+176=0\\\\\\\textrm{We get}\\\\x^2-30x+176=\left(x-8\right)\left(x-22\right)\\\\`

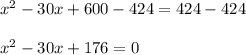
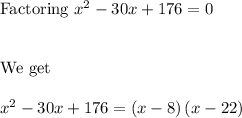
This is a quadratic equation which can be solved using the quadratic formula or by factoring

`\textrm{Factoring } x^2-30x+176=0\\\\\\\textrm{We get}\\\\x^2-30x+176=\left(x-8\right)\left(x-22\right)\\\\`

So

`x^2-30x+176=0 \rightarrow (x -8)(x-22) = 0\\\\`

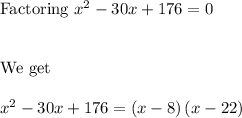
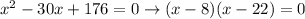
So x = 8 or x = 22 are two possible solutions to this quadratic

If x = 22, it will be greater than the width of 20 and also 20-x = -2 so it is not a valid solution for this situation

Therefore we get the final answer as
`\boxed{x = 8 \;m}`