Question

Polynomial Arithmetic

Polynomial 1: 2x2
+ 3x − 6
Polynomial 2: x2
− 4x + 2
Question 1



What is the sum of the two polynomials?
Responses


A x2
− x − 4x 2 − x − 4


B 3x2
− x + 43 x 2 − x + 4


C 3x2
− x − 43 x 2 − x − 4


D x2
− x + 2x 2 − x + 2
Question 2



What is the product of the two polynomials?
Responses


A 4x4
− 5x3
− 14x2
+ 30x + 124 x 4 − 5 x 3 − 14 x 2 + 30x + 12


B 2x4
− 5x3
+ 7x2
+ 15x + 122 x 4 − 5 x 3 + 7 x 2 + 15x + 12


C 2x4
− 5x3
− 14x2
+ 30x − 122 x 4 − 5 x 3 − 14 x 2 + 30x − 12


D 8x4
− 5x3
+ 14x2
+ 45x − 12

Answer 1

Sum of two polynomials:

`3x^2 - x - 4` Choice C (read explanation carefully)

Product of the two polynomials:

`2x^4-5x^3-14x^2+30x-12\\\\` Choice C (read explanation carefully)

In both cases, your answer choice copy/paste messed up the formatting. I looked at the coefficients and came up with the choices.

You should compare the actual terms with the choices I have provided to make sure they match

Explanation:

The two polynomials are
2x² + 3x - 6

and

x² - 4x + 2

Addition

To add these two polynomials together group like terms and add their coefficients:

(2x² + 3x - 6) + (x² - 4x + 2)

= 2x² + 3x - 6 + x² - 4x + 2

= (2x² + x²) + (3x -4x) + (-6 + 2)

= 3x² - x - 4

Your answer choices have lost formatting during copy paste. You will have to compare and choose the right one. I think it is C because it has a 3x² term and the last term is - 4

Multiplication

`\left(2x^2\:+\:3x\:-\:6\right)\cdot \left(x^2-4x\:+\:2\right)\\\\\\`
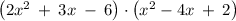
Distribute the parentheses - multiply each term in the second polynomial by each term in the first polynomial and simplify

`\left(2x^2\:+\:3x\:-\:6\right)\cdot \left(x^2-4x\:+\:2\right)\\\\= 2x^2x^2+2x^2\left(-4x\right)+2x^2\cdot \:2+3xx^2+3x\left(-4x\right)+3x\cdot \:2-6x^2-6\left(-4x\right)-6\cdot \:2\\\\= 2x^4-8x^3+4x^2+3x^3-12x^2+6x-6x^2+24x-12\\\\\textrm{Add similar terms}\\=2x^4 +(-8x^3+3x^3)+ (4x^2-12x^2-6x^2) + (6x+24x) -12\\\\`

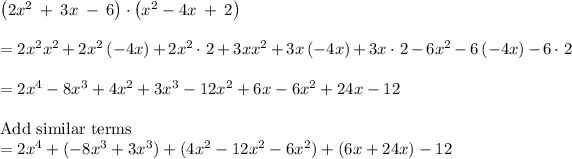
`=2x^4-5x^3-14x^2+30x-12\\\\` (Answer)

Again your answer choices have lost formatting but my best guess from looking at the coefficients is that it is choice C