Question

How do i solve? im studying so please be detailed

Answer 1

26. Scale Factor of A to B:
`\boxed{(3)/(4)}`

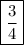
27. Scale factor of B to A:
`\boxed{(4)/(3)}`

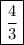
Explanation:

If two triangles are similar, the ratios of the side length to the corresponding side length of the other must be the same for all sides

The first challenge is to figure out which side of triangle A corresponds to which side of triangle B

If you flip triangle A counterclockwise by 90° the angles will be aligned with each other and it is easier to see the corresponding sides of A and B

We see that ....

side length 24 of A matches with side length 18 of B

side length 36 of A matches with side length 27 of B

side length 32 of A matches with side length 24 of B

B is of smaller size than A so the scale factor of A to B is less than 1

26.

Therefore the scale factor of A to B is

`(18)/(24) = (27)/(36) =(24)/(32)\\\\\\(18)/(24)= (3)/(4) \cdots \textrm { by dividing numerator and denominator by 6}`

`(27)/(36) = (3)/(4) \cdots \textrm { by dividing numerator and denominator by 9}\\\\\\(24)/(32) = (3)/(4) \cdots \textrm { by dividing numerator and denominator by 8}\\\\\\`

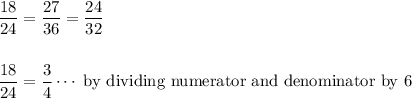
So the scale factor of Figure A to Figure B is
`(3)/(4)`

----------------------------------------------------------------------------------------------

27.

The scale factor of Figure B to Figure A is the reciprocal of

`(3)/(4)`

Reciprocal of

`(3)/(4) \; is \; (4)/(3)`

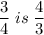
So scale factor of B to A is

`(4)/(3)`