Question

How to simplify rational expressions in algebra 2It's x^2, not x^3

Answer 1

`f(x)=(x^2-7x+12)/(9-x^2)`

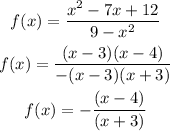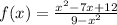
Applying the quadratic formula to the polynomial in the numerator, we get:

`\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{7\pm\sqrt[]{(-7)^2-4\cdot1\cdot12}}{2\cdot1} \\ x_(1,2)=\frac{7\pm\sqrt[]{1}}{2} \\ x_1=(7+1)/(2)=4 \\ x_2=(7-1)/(2)=3 \end{gathered}`

Where x1 and x2 are the roots of the polynomial.

Therefore, this polynomial can be expressed as follows:

`\begin{gathered} ax^2+bx+c=a(x-x_1)(x-x_2)^{} \\ x^2-7x+12=1(x-3)(x-4) \\ x^2-7x+12=(x-3)(x-4) \end{gathered}`

To find the roots of the polynomial in the denominator we have to solve the equation in which the denominator is equal to zero, that is,

`\begin{gathered} 9-x^2=0 \\ 9=x^2 \\ \sqrt[]{9}=x \\ \text{ This square root has two solutions:} \\ x_1=3 \\ x_2=-3 \end{gathered}`

Using the roots, the polynomial can be expressed as follows:

`\begin{gathered} ax^2+bx+c=a(x-x_1)(x-x_2)^{} \\ -x^2+9=-1(x-3)(x-(-3)) \\ -x^2+9=-(x-3)(x+3) \end{gathered}`

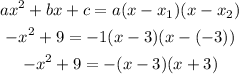
Substituting these equivalent expressions into the original rational expression, and simplifying, we get:

`\begin{gathered} f(x)=(x^2-7x+12)/(9-x^2) \\ f(x)=((x-3)(x-4))/(-(x-3)(x+3)) \\ f(x)=-((x-4))/((x+3)) \end{gathered}`