Part A.
In this case, we need to find the perimeter of the figure, which is equal to the lenght of the three side and the semicircle.
Since the arc of the semicircle has a lenght of one half the circunference,

where, in our case, the radius is
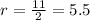
then, the arc lenght of the semicircle is3
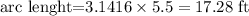
Therefore, the Perimeter of the figure is
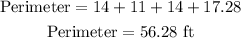
Therefore, the answer for part A is 56.28 feet.
Part B.
In this case, we need the area of the semicircle and the area of the rectangle below it, that is,
The area of the semicircle is half the area of the circle, that is,
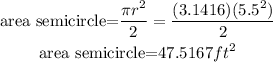
and the area of the rectangle is
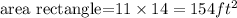
Therefore, the total area is
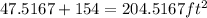
Therefore, the answer for part B is: 204.52 square feet