Answer:
a) P = 0.0995
b) P = 0.9975
c) μ = 4.5
σ = 1.57
Step-by-step explanation:
To find the probabilities, we will use the binomial distribution because we have 10 identical events with a probability of 45% to success. Then, the probability that x students rent their textbook is calculated as
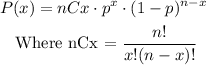
Where n = 10 and p = 0.45, so
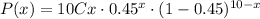
Then, the probability that no more than 2 rent their book is equal to

Now, we can calculate the probability that at least one does as
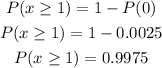
Finally, the mean and standard deviation in a binomial distribution is equal to
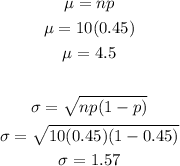
Therefore, the answers are
a) P = 0.0995
b) P = 0.9975
c) μ = 4.5
σ = 1.57