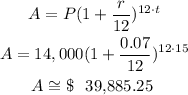Question

If $14,000 is invested in an account for 15 years. Calculate the total interest earned at the end of 15years if the interest is:(a) 7% simple interest: $(b) 7% compounded annually: $(c) 7% compounded quarterly: $(d) 7% compounded monthly: $Round your answers to the nearest cent.

Answer 1

Hello!

Let's solve alternative (a):

For simple interest, we'll use the formula below:

`A=P(1+(r)/(100)\cdot t)`

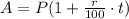
Let's replace them with the values:

`\begin{gathered} A=14,000(1+0.07\cdot15) \\ A=14,000(1+1.05) \\ A=14,000\cdot2.05 \\ A=\$28,700 \end{gathered}`

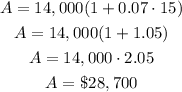
Solving alternative (b):

To compound interest, we'll modify the formula:

`A=P(1+(r)/(100))^t`

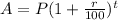
So, we'll have:

`\begin{gathered} A=14,000(1+0.07)^(15) \\ A=14,000(1.07)^(15) \\ A=14,000\cdot2.75903 \\ A=\$\text{ }38,626.42 \end{gathered}`

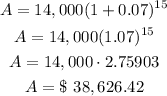
Solving alternative (c):

`\begin{gathered} A=P(1+(r)/(4))^(4t) \\ A=14,000(1+(0.07)/(4))^(4\cdot15) \\ A=14,000(1.0175)^(60) \\ A\cong$ \$\text{ }39,645.43 $ \end{gathered}`

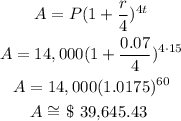
Solving alternative (d):

`\begin{gathered} A=P(1+(r)/(12))^(12\cdot t) \\ A=14,000(1+(0.07)/(12))^(12\cdot15) \\ A\cong\$\text{ }$ 39,885.25 $ \end{gathered}`