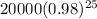Question

2) In 2000, the population of a town in 20,000 and decreased by 2% each year.

a) Write an equation to model this scenario.

b) What will the population be in 2025?

Answer 1

a) General Equation for this scenario is


`\boxed{P_n = P(.98)^n\\\\}`

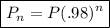
where P is the starting population and Pₙ is the population at the end of n years

For this specific case,

`\boxed{P_n = 20000(0.98)^n}`

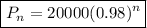
b) Population in 2025 will be the population after 25 years:

`P_(25) = 20000(0.98)^(25) = \boxed{12,069}`

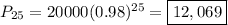
Explanation:

In general, if the population at year 0 is P and it decreases by 2% each year then the population after one year will be given by

P - decrease in one year

Decrease in population for 1 year = 2% of P
`= 0.02P`

So P(after 1 year) :

`P - 0.02P\\\\ = P(1-0.02) \\\\= 0.98P`

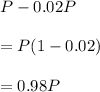
After 2 years the population will be population after 1 year (0.98P) - decrease in population for 1 year (0.02 x 0.98P)

So population at end of 2 years would be

`0.98P - 0.98P(0.02)\\\\= 0.98P(1-0.02)\\\\=0.98P(0.98)\\\\= P(0.98)^2`

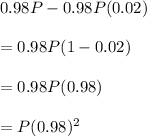
In general after n years the population would be

`P(0.98)^n\\\\`

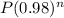
If the population in year 2000 is 20,000 then population at the end of 25 years is:


`20000(0.98)^(25)`

`\rm\:{=\:12,069\:\;\:rounded\:down\:to\:the\:nearest\:integer}`