Question

An election ballot asks voters to select six city commissioners from a group of twenty two candidates. In how many ways can this be done?

Answer 1

In this case, we have 6 places to fill from a pool of 22 candidates. There is no difference in the places: they are all commissioners, so if candidate A is selected, the order does not matter, but there is only one candidate, so there is no repetition.

Then, this is a combination (as the order does not matter) with no repetition of 22 elements in 6 places.

We can calculate this as:

`\begin{gathered} C(n,r)=(n!)/(r!(n-r)!) \\ C(22,6)=(22!)/(6!(22-6)!)=(22!)/(6!\cdot14!)=(22\cdot21\cdot20\cdot19\cdot18\cdot17\cdot16\cdot15)/(6\cdot5\cdot4\cdot3\cdot2\cdot1)=17907120 \end{gathered}`

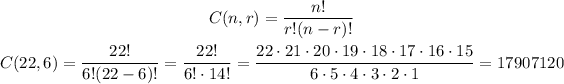
Answer: there are 17,907,120 ways this can be done.