Question

Two identical 6.8kg balls are in contact with one another. The gravitational attraction between the balls is 6.2E-08 N A. What is the radius of one of these balls?

Answer 1

Given that the mass of each ball is m = 6.8 kg

The distance between them is d = 2r

Here, r is the radius of the ball.

The gravitational force of attraction is

`F=\text{ 6.2}*10^(-8)\text{ N}`

We have to find the radius of the ball.

The gravitational force formula is

`F=(Gmm)/((2r)^2)`

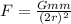
Here, the universal gravitational constant is

`G=\text{ 6.67}*10^(-11)Nm^2kg^(-2)`

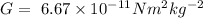
The radius will be

`\begin{gathered} r=\sqrt[]{(Gmm)/(4F)} \\ =\sqrt[]{(6.67*10^(-11)*6.8*6.8)/(4*6.2*10^(-8))} \\ =\text{ 0.114 m} \end{gathered}`

Thus, the radius of one of these balls is 0.114 m