To match the equation with its solution set we need to solve each of them. Let's do that
First equation:
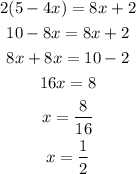
Second equation:
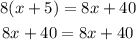
Since both sides of the equation are exactly the same expression we conclude that this equation is satisfied by all real numbers.
Third equation:
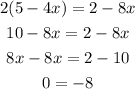
Since the last line is a contradiction we conclude that this equation has no solutions.
Fourth equation:
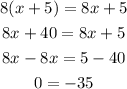
Once again we have a contradiction in the last line, then this equation has no solutions.
Then the correct match is:
First equation with c.
Second equation with b.
Third equation with a.
Fourth equation with a.