Question

a normal distribution has a mean of 31 and a standard deviation of 3. Find the percentage of data values that are in the given intervals.

Answer 1

The percentage of values between 25 and 34 is 81.5%

Here, we want to get the percentage of data values in the given interval

To do this, we proceed as follows;

Firstly, we will need to get the z-values for each of the points

To do this, we are going to use the z-score formula;

`\begin{gathered} z\text{ = }(x-\mu)/(\sigma) \\ \\ \mu\text{ = mean = 31} \\ \sigma\text{ = standard deviation = 3} \\ \\ \text{For x = 25;} \\ z\text{ = }(25-31)/(3)\text{ = }(-6)/(3)\text{ = -2} \\ \text{For x = 34} \\ z=\text{ }(34-31)/(3)\text{ = }(3)/(3)\text{ = 1} \end{gathered}`

Now, we have to find the probability between the two z-scores

We have this as the percentage of values from two standard deviation below the mean to 1 standard deviation above the mean

We can get this from the normal distribution curve;

The addition of the values here are;

`0.34\text{ + 0.34 + 0.135 = 0.815}`

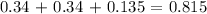
Writing this probability as a percentage, we have 81.5%