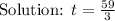Question

Solve the radical equation. Be sure to check all solutions to eliminate extraneous solutions.sqrt(3t+5)=8

Answer 1

Given the Radical Equation:

`√(3t+5)=8`

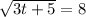
• You can solve it as follows:

1. Square both sides of the equation in order to undo the effect of the square root, because, by definition:

`(\sqrt[]{b})^2=b`

Then:

`\begin{gathered} (√(3t+5))=(8)^2 \\ \\ 3t+5=64 \end{gathered}`

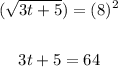
2. Apply the Subtraction Property of Equality by subtracting 5 from both sides of the equation:

`\begin{gathered} 3t+5-(5)=64-(5) \\ \\ 3t=59 \end{gathered}`

3. Apply the Division Property of Equality by dividing both sides of the equation by 3:

`\begin{gathered} (3t)/(3)=(59)/(3) \\ \\ t=(59)/(3) \end{gathered}`

• In order to check the solution, you need to substitute it into the original equation and evaluate it. If both sides of the equation are equal, then the equation is true:

`\sqrt[]{3((59)/(3))+5}=8`
`\sqrt[]{(59\cdot3)/(3)+5}=8`
`\sqrt[]{59+5}=8`
`\begin{gathered} \sqrt[]{64}=8 \\ \\ 8=8\text{ (True)} \end{gathered}`

Hence, the answer is:

`\text{Solution: }t=(59)/(3)`