Question

Jimmy invests $500 in an account with a 3% interest rate, making no other deposits or withdrawals. What will Jimmy’s account balance be after 10 years if the interest is compounded 2 times each year? $673.43$173.43$903.06$580.27

Answer 1

For us to be able to determine Jimmy's account after 10 years, we will be using the Compounded Interest Formula:

`A=P(1+(r)/(n))^(nt)`

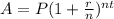
Where,

A=final amount

P=initial principal balance

r=interest rate (in decimal)

n=number of times interest applied per time period

t=number of time periods elapsed (in years)

Given:

P = $500

r = 3% = 3 ÷ 100 = 0.03

n = compunded semi-anually = 2

t = 10 years

We get,

`A=P(1+(r)/(n))^(nt)`
`=500(1+(0.03)/(2))^(2(10))`
`=500(1+0.015)^(20)`
`=500(1.015)^(20)`
`=500(1.3468550065500560376005930177624)`
`=673.42750327502801880029650888121`
`\text{ }\approx\text{ \$673.43}`

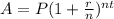
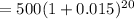
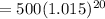
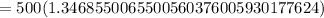
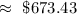
Therefore, the answer is letter A - $673.43