Question

Please help me I'm struggling very muchx^3+14x^2+48x=0

Answer 1

x = - 8, x = - 6, x = 0

Explanation:

x³ + 14x² + 48x = 0 ← factor out x from each term

x(x² + 14x + 48) = 0 ← factor the quadratic

consider the factors of the constant term (+ 48) which sum to give the coefficient of the x- term (+ 14)

the factors are + 8 and + 6 , then

x(x + 8)(x + 6) = 0

equate each factor to zero and solve for x

x = 0

x + 8 = 0 ⇒ x = - 8

x + 6 = 0 ⇒ x = - 6

Answer 2

The solutions are:

• x = 0

,

• x = -6

,

• x = -8

EXPLANATION

First we can see that there's and x in every term of the polynomial, so one of the solutions to the equation is when x = 0, because x is a common factor:

`\begin{gathered} x^3+14x^2+48x=0 \\ x(x^2+14x+48)=0 \end{gathered}`

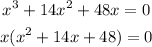
The other two solutions - we know that there are three because the degree of the polynomial is 3 - are the zeros of the polynomial in parenthesis. We can solve it with the formula:

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In our polynomial, a = 1, b = 14 and c = 48:

`\begin{gathered} x=\frac{-14\pm\sqrt[]{14^2-4\cdot48}}{2} \\ x=\frac{-14\pm\sqrt[]{196-192}}{2} \\ x=\frac{-14\pm\sqrt[]{4}}{2} \\ x=(-14\pm2)/(2) \\ x_1=(-14-2)/(2)=(-16)/(2)=-8 \\ x_2=(-14+2)/(2)=(-12)/(2)=-6 \end{gathered}`

Therefore the solutions to the equation are x = 0, x = -8 and x = -6