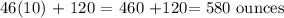Question

water is added to two containers for 15 minutes the equation below model the ounces of water Y in each container after X minutes at the time when the containers hold the same amount of water how much water do they hold container a y equals 46x + 120 container b y equals negative 2x ^ 2 + 60x + 180

Answer 1

The amount of water each will hold at a time when they hoild equal amount of water is 580 ounces

Here, we want to know the amount of water that will be present in both containers when they hold the same amount of water

What we have to do here is to equate the y-values

Thus, we have it that;

`\begin{gathered} 46x+120=-2x^2+60x+180 \\ 46x+120+2x^2-60x-180=0 \\ 2x^2+46x-60x+120-180\text{ = 0} \\ 2x^2-14x-60\text{ = 0} \\ \\ Divide\text{ through by 2} \\ x^2-7x-30\text{ = }0 \\ x^2-10x+3x-30\text{ = 0} \\ x(x-10)\text{ +3(x-10) = 0} \\ (x+3)(x-10_{})\text{ = 0} \\ x\text{ + 3 = 0 or x-10 = 0} \\ x\text{ = -3 or x = 10} \end{gathered}`

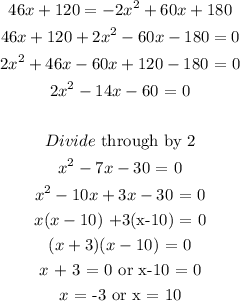
Since time cannot be negative, we only will select 10 as our answer

To know the amount of water, what we have to do is to substitute the value of x in any of the equations for y

We have this as;

`46(10)\text{ + 120 = 460 +120= 580 ounces}`